고정 헤더 영역
상세 컨텐츠
본문
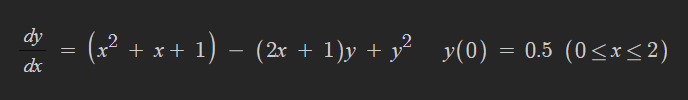
위 미분방정식의 초기값 문제를 오일러법과 4차 룽게 쿠타법을 이용해 풀어보겠습니다.
📣 오일러법의 알고리즘
1. f(x,y), a, b, c, n을 지정 (구간 [a,b]를 n등분, c는 초기값)
2. h = (b-a)/n, x0 =a, y0 = c
3. j=0, ,1, 2, ..., n에 대해서 다음 계산을 실행
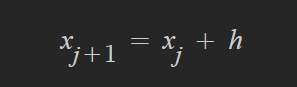

오일러 방법으로 푸는 알고리즘은 euler 함수 안에 구현함
📣 4차 룽게 쿠타법의 알고리즘
1. f(x,y), a, b, c, n을 입력
2. h=(b-a)/n, x0 = a, y0 = c
3. j = 0,1,2,...,n 에 대해서 다음 계산을 실행

룽게 쿠타법을 이용한 풀이는 runge 함수안에 구현함
n값이 20인 이유는 구간을 나눈 폭(= h값)을 0.1로 설정하기 위해서임 (0~2 구간을 20으로 나누면 0.1)
🚩 출력결과
x[i] euler runge exact
0.00 0.500000 0.500000 0.500000
0.10 0.575000 0.575021 0.575021
0.20 0.650063 0.650166 0.650166
0.30 0.725312 0.725557 0.725558
0.40 0.800870 0.801312 0.801312
0.50 0.876852 0.877541 0.877541
0.60 0.953369 0.954344 0.954344
0.70 1.030519 1.031812 1.031812
0.80 1.108391 1.110026 1.110026
0.90 1.187063 1.189051 1.189051
1.00 1.266597 1.268942 1.268942
1.10 1.347045 1.349740 1.349740
1.20 1.428443 1.431475 1.431475
1.30 1.510818 1.514165 1.514165
1.40 1.594180 1.597816 1.597816
1.50 1.678533 1.682426 1.682426
1.60 1.763867 1.767982 1.767982
1.70 1.850166 1.854465 1.854465
1.80 1.937404 1.941851 1.941851
1.90 2.025552 2.030109 2.030109
2.00 2.114573 2.119203 2.119203
알고리즘 출처 : サイエンス社 数値計算入門 140p, 144p
프로그램은 내가 직접 작성. 잘못된 부분 있으면 덧글로 알려주세요.
'IT > C' 카테고리의 다른 글
| C언어 최소제곱법을 이용해 직선과 상관계수 구하기 (0) | 2021.01.02 |
|---|---|
| C언어 텍스트, 바이너리 파일 읽기 쓰기 (2) | 2020.12.02 |
| C언어 수치계산 - 다항식 계산 알고리즘 (호너법 Horner's method) (2) | 2020.11.23 |
| C언어 수치계산 수치적분 (구분구적법, 사다리꼴, 심슨 공식) (0) | 2020.09.03 |
| C언어 예제 두 수의 합 구하기 (0) | 2020.06.04 |





댓글 영역